√画像をダウンロード 二 等辺 三角形 定理 252209

 古代ギリシャの数学者タレスの名を冠する定理は5つあります。 タレスの功績にも触れながら、それぞれの定理について解説していきます。 Ⅰ 最も有名なタレスの定理 古代ギリシャの数学者タレス（Thales, BC625頃BC547頃）は、ピラミッドの高さの測量や日食の予言でよく知られ、二等辺三角形の定理は 「二等辺三角形の2つの底角は等しい」 二等辺三角形の定理は 「二等辺三角形の頂角の二等分線は、 底辺を垂直に2等分する。」 正三角形の定義は 「3辺が等しい三角形」 正三角形の定理は 「正三角形の3つの角は等しい」 三角形の定理初等幾何学における ピタゴラスの定理 （ ピタゴラスのていり 、 （ 英 Pythagorean theorem ）は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 （ さんへいほうのていり ） 、 勾股弦の

Studydoctor二等辺三角形や台形の面積と三平方の定理 中学３年数学 Studydoctor

二 等辺 三角形 定理

二 等辺 三角形 定理-② 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 ③ 二辺の長さが等しい三角形は二等辺三角形である。 直角三角形 合同条件 ① 斜辺と1つの鋭角がそれぞれ等しいとき、2つの直角三角形二等辺三角形 足が5本（正五角形？ ）の椅子を購入することを考えてます。 足の横幅で、最長の幅は記載があるが、最小の幅の記載がない。 がないため2等辺三角形の高さが最小幅と考えネットで公式はたくさん出てくるが自分で計算できなかったのでお

三角形のペア 大田 桐光本部校 ブログ

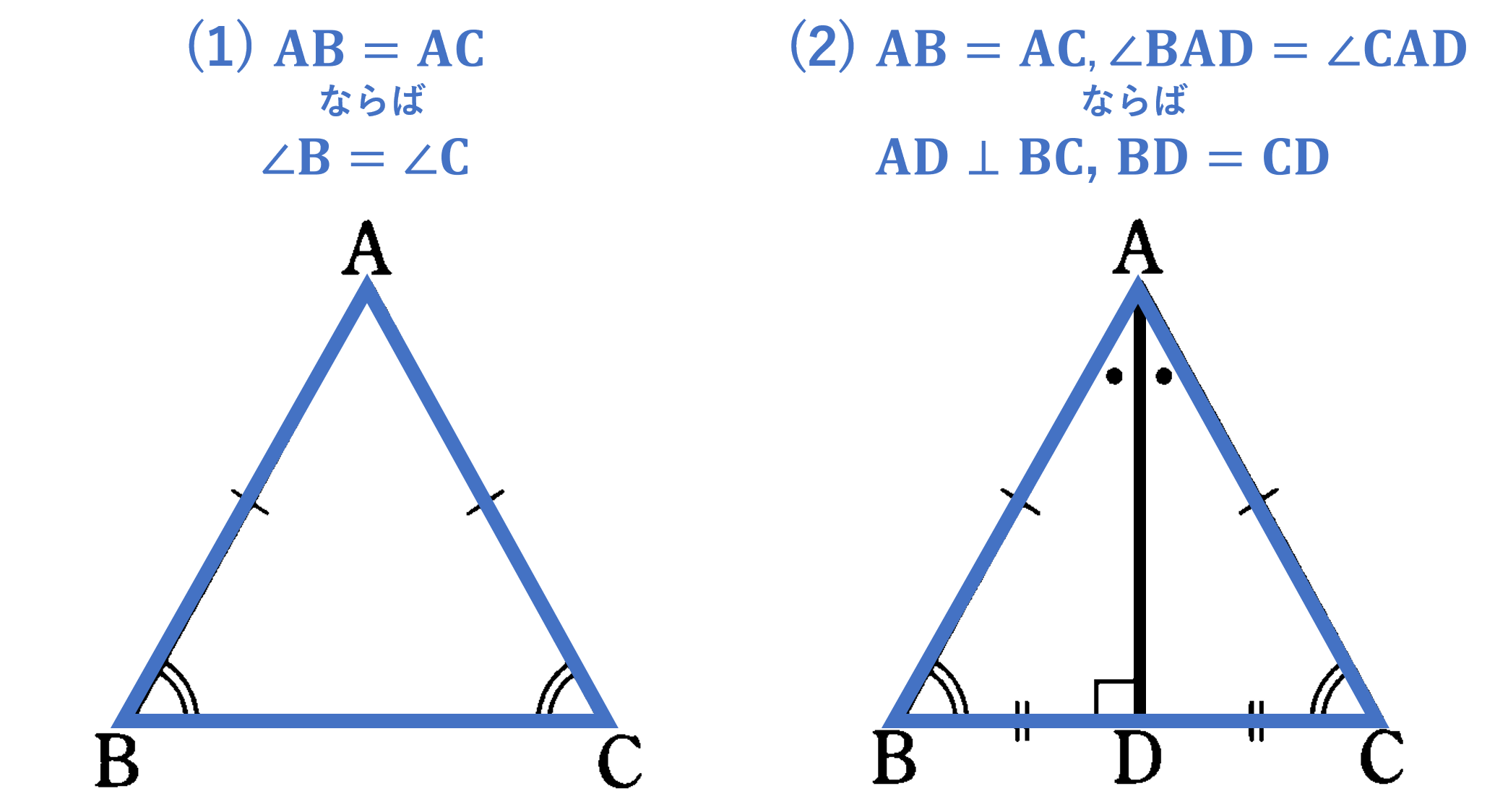
二等辺三角形の頂角の二等分線は， 底辺を垂直に2 等分する さが等しい 1組の対辺が平行でその長 四角形は、平行四辺形 2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの身近な三平方の定理といえば、小学校からよく使う2つの三角定規です。 直角二等辺三角形の定規の辺の比は、11 √2（内角は、90°、45°、45°） この場合、斜辺が√2です。 1² ＋ 1² =√2²二等辺三角形の高さの求め方 まとめ 二等辺三角形の高さを求めるためには まず、頂角からまっすぐな線を引きましょう！ すると、直角三角形を作ることができるので そこから三平方の定理を使ったり 角度がわかる場合には比を取って 高さを求めてき

 三角形 \(abc\) について、点 \(a,b,c\) の内角をそれぞれ角 \ とおいたときに、以下の3つの式が成り立つことを 余弦定理 2倍角の公式・半角の公式とその証明。二等辺三角形で分かる2倍角の考え方直角二等辺三角形の底辺と高さの長さは同じです。 底辺（高さ）の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11＝2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1：1；√2」です。 今回は、直角 そして 命題a「二等辺三角形の底辺は等しい」 は非常に基礎的な定理です。 流石に，三角形の合同条件のうち 二辺夾角相等 は，命題a より先の定理ですが， 三角形の合同条件の三辺相当 や， 角の二等分線を引ける 線分の中点を作図できる などは，命題a

 二等辺三角形のかき方は正三角形をかく過程での 失敗の中から学ぶことができる。失敗を生かした授 業を構成できるのである。 この後は、円周上に点の無い円を使って正三角形 をかき、最後は円を使わずにコンパスを使って正三 角形、二等辺三角形を作図していく。三角形 面積 大きな数 二等辺三角形は、2つの底角が等しい定理 二等辺三角形は、頂角の二等分線は底辺を垂直に2等分する定理 正三角形は、3辺が等しい三角形定義 正三角形は、3つの内角が等しく、すべて60°定理 直角三角形は、1つの角が直角である三角形二等辺三角形の定義と性質 定義 2辺の長さが等しい三角形 定理（性質） 底角が等しい 頂角の二等分線は底辺を二等分するに垂線になる ここでいう定義とは、「こういう三角形を二等辺三角形としよう」と決めたことなので、これは導くことができませ

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

二等辺三角形の定義と定理

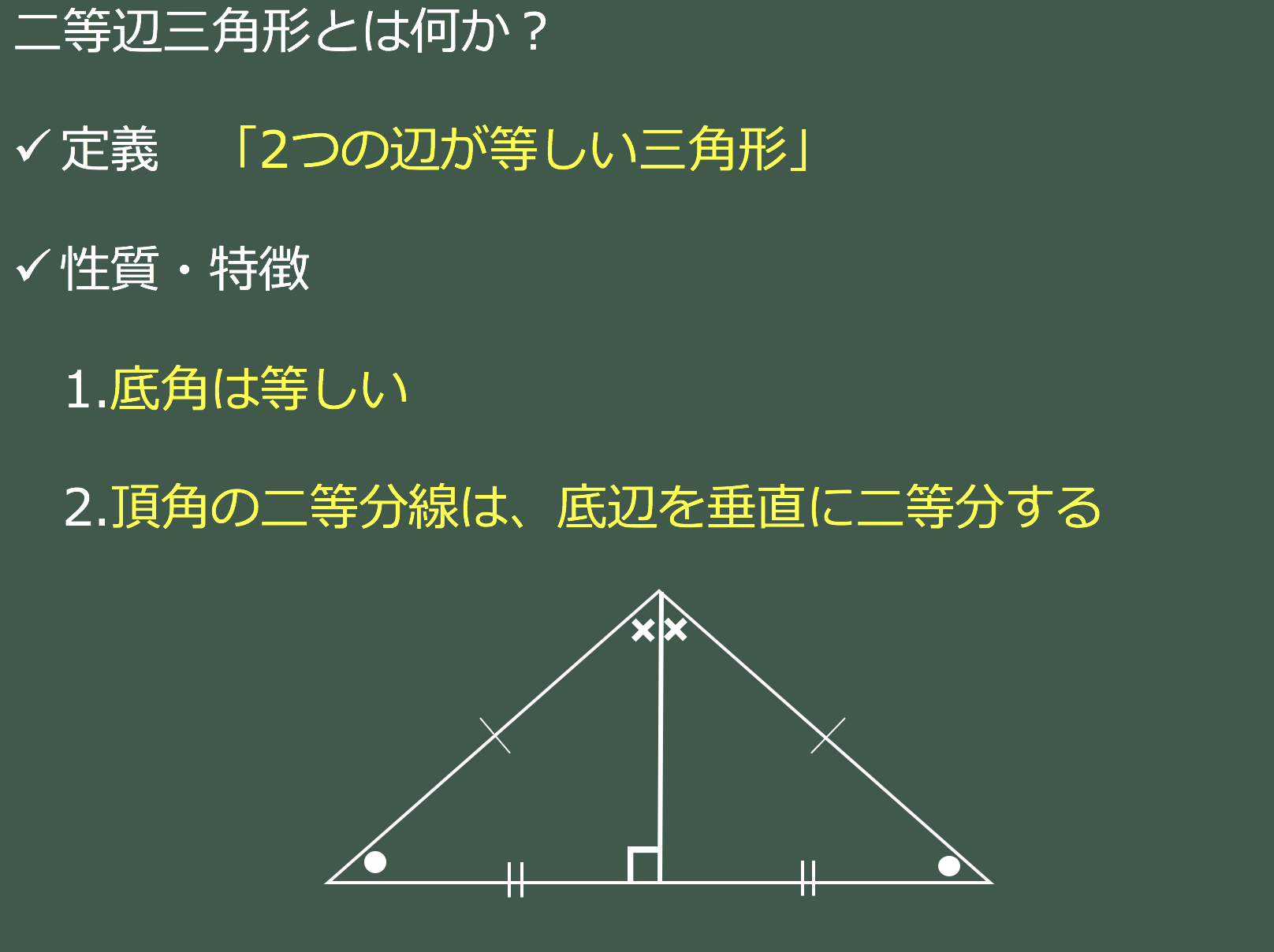
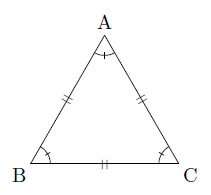
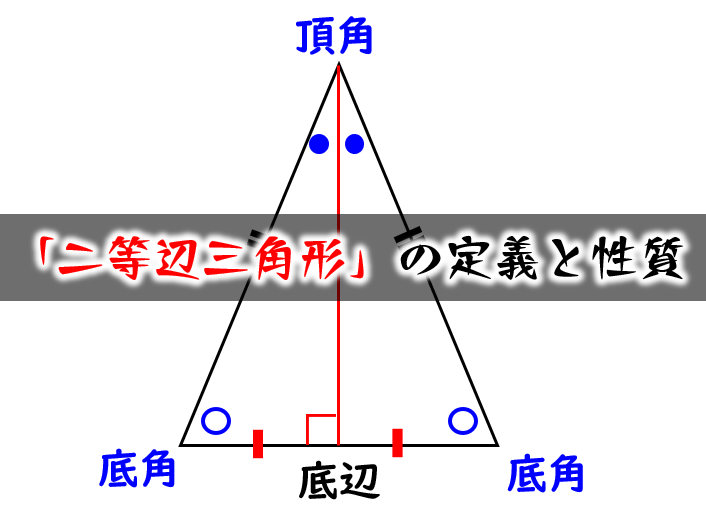
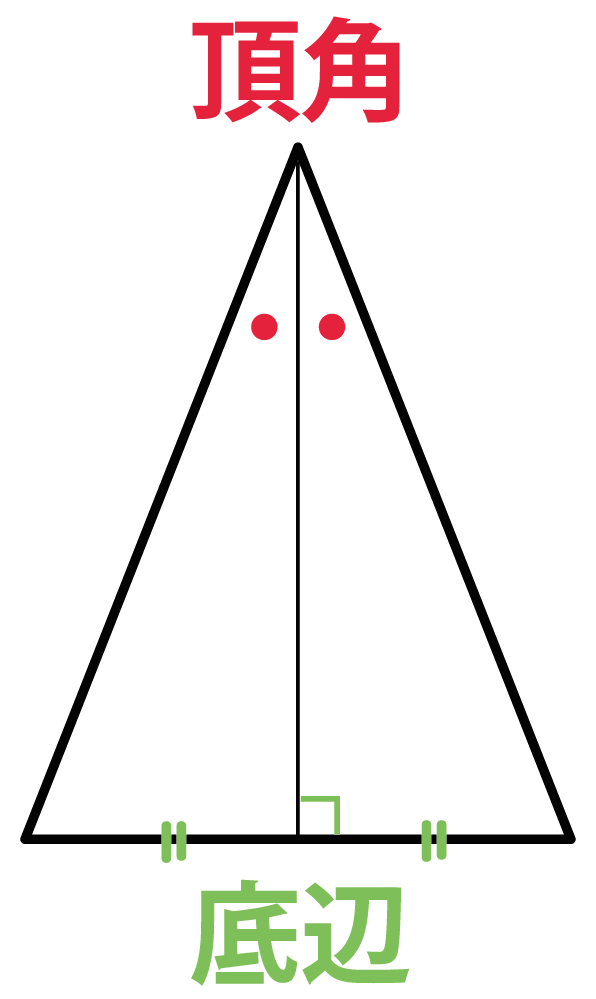
二等辺三角形の定義と性質 定義 2辺が等しい三角形 図のように二等辺三角形で等しい2辺 (ABとAC)の間の角を 頂角 頂角以外の2角を 底角 、頂角の対辺を 底辺 という。 A B C 底角 底角 頂角 底辺 定理 二等辺三角形の底角は等しい。 >>証明 kiepert（キエペルト，キーペルト）の定理： 三角形 a b c abc a bc の外側（または内側）に相似な二等辺三角形 a b f, b c d, c a e abf,bcd,cae a bf, bc d, c a e をつくる。このとき， a d, b e, c f ad,be,cf a d, be, cf は一点 x x x で交わる。「定理」とよばれている代表的なものは「円周角の定理」，「三平方の定理」です。 例として「二等辺三角形」で説明してみましょう。 定義二辺が等しい三角形 (図の三角形abcでab=ac) ここで紹介している内容は17年3月時点の情報です。

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

Ed City Daito Osaka Jp

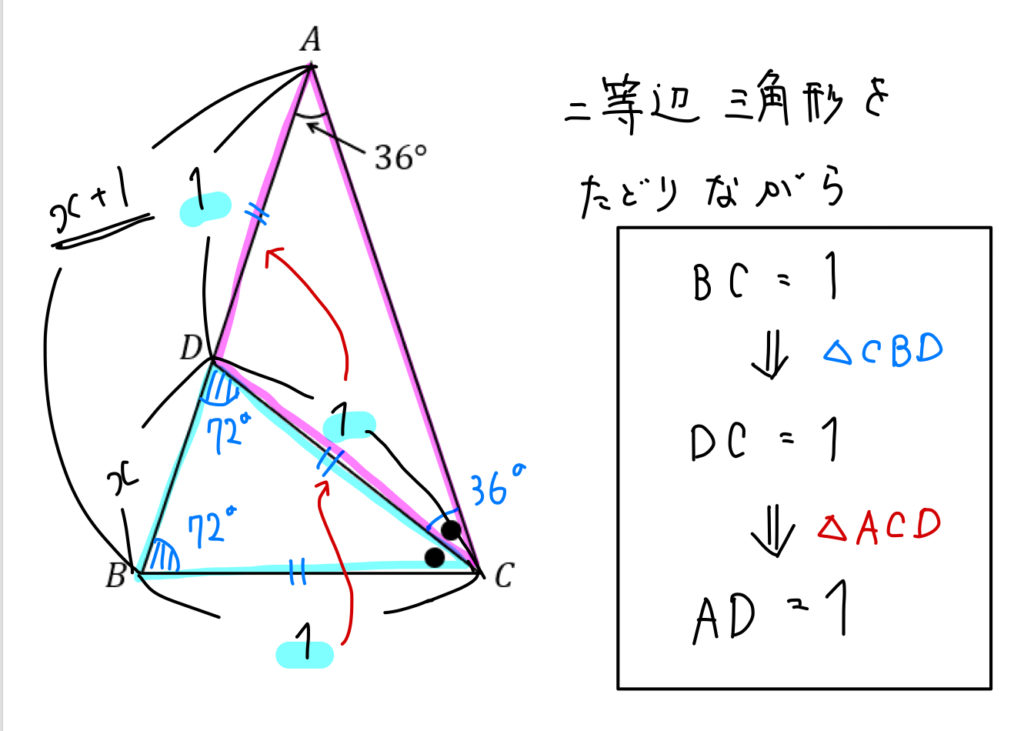
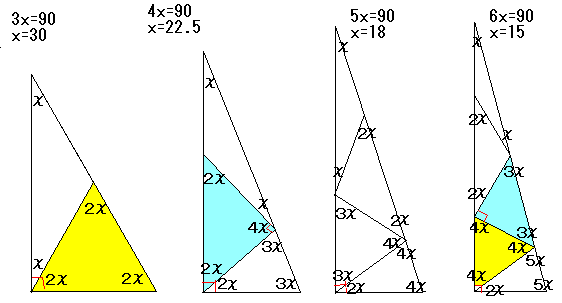
A＝90゜の直角二等辺三角形 B＝90゜の直角二等辺三角形 C＝90゜の直角二等辺三角形 (2) A(2,5), b(1,3), C(0,2) AB＝BCの二等辺三角形 BC＝CAの二等辺三角形 CA＝ABの二等辺三角形 正三角形 A＝90゜の直角三角形それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、よく利用することになるので覚えておきましょう。 30°、60°、90°の直角三角形→辺の長さの比は\(1：2：\sqrt{3}\) 三角形の辺の長さの比が\(1：2：\sqrt{3}\)→ 30°、60°、90°の直角三角形 水色の三角形が、2角が等しいので二等辺三角形になることが分かります。すると、 赤の二等辺三角形が見えてきます。ここまでくれば、70°=x40°が分かるので、 x=30° と求まります！！ 実に鮮やかに二等辺三角形が次々に出来ていく様が爽快ですね。 1

二等辺三角形の定理の証明とその利用

3

定義 2つの辺の長さが等しい三角形を二等辺三角形という。 定理 二等辺三角形の2つの底角の大きさは等しい。 定理 二等辺三角形の頂角の二等分線は底辺を垂直に2等分する。 定理 二等辺三角形の底辺の垂直二等分線は頂角を通る。 定理Ama04 練習問題へ abdu は直角二等辺三角形，u bcd は30 °，60 °の角をもつ直角三角形であるから，3 辺 のうちの1 辺の長さがわかると残りの辺の長さも求められる。 ここでは，共通のbd の長さを 調べると，xの値が求められる。 abhu とu ach に分けて，それぞれがどのような辺の比をもつ二等辺三角形（にとうへんさんかくけい、英 isosceles triangle ）は、三角形の一種で、3 本の辺のうち（少なくとも）2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。

５章 三角形と四角形 タカラゼミ

世界に1つだけの三角形の組 大学院生が定理の証明に成功 数理女子

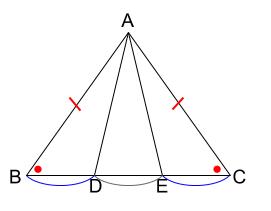
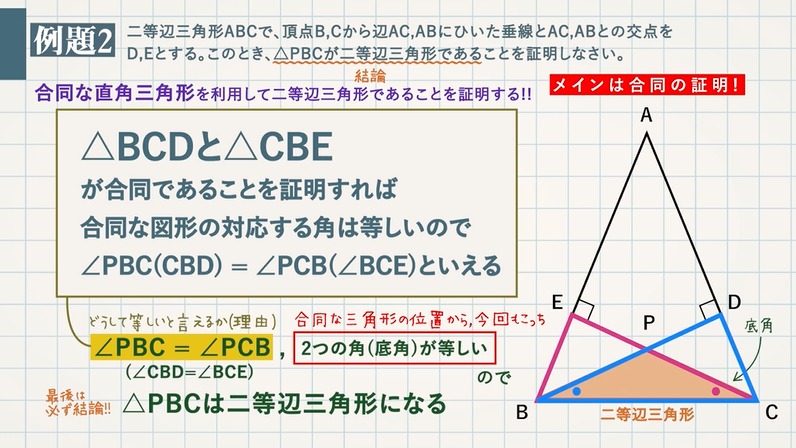
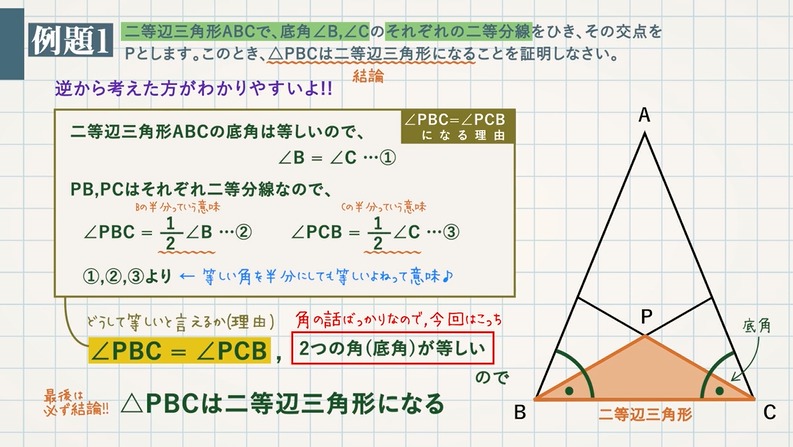
 二等辺三角形の定義、定理、基本的な証明問題の練習プリントです。定期テストにもよく出題されますので、確実に出来るようにしましょう。 二等辺三角形の定義「二つの辺の長さが等しい三角形」 等しい二辺の間の角を頂角という。 頂角に向い合う辺を底辺という。 二等辺三角形がある」問題です PABが二等辺三角形なので ∠ P B A = ∠ P A B ＝ x ですね ABPの外角に注目して ∠ B P C = ∠ P B A ＋ ∠ B A P ＋ ＝ = x ＋ x ＝ 2 x ABCは二等辺三角形なので ∠ A B C = ∠ A C B ＝ 2 x です ABCの内角の和で方程式を立てて送信を完了しました。 直角二等辺三角形 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に

二等辺三角形と証明 中学２年 数学クラブ

中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su

したがって efgは二等辺三角形となる。 確認 四角形abcdで、p,rはそれぞれ辺ad, bcの中点、q,sはそれぞれ対角線bd,acの中点である。 答表示 a b二等辺三角形の面積 例題 ABCの面積を求める。 A B C 13cm 13cm 10cm ABCは二等辺三角形なので,頂点Aから辺BCに 垂線ADを引くとDはBCの中点になる。 A B C 13cm 13cm D 5cm よって、BD=5cm、 ABDで三平方の定理より AD 2 5 2 =13 2 AD 2 = 144 AD>0よりAD=12 面積 =10×12÷2

تويتر 中学高校数学laf先生 質問回答中 على تويتر 中2数学 二等辺三角形の性質 ここでは 定義 と 定理 という小難しい言葉が出てきますね O O 定義 言葉の意味を丁寧に説明したものだよ 二等辺三角形の定義 二つの辺が等しい

Ed City Daito Osaka Jp

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

二等辺三角形になることの証明 Youtube

3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ

正三角形の性質 まなびの学園

二等辺三角形の定義と定理 算数 数学が好きになりmath

直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

シュタイナー レームスの定理

中3数学 三平方の定理 二等辺三角形の面積 Youtube

正三角形や二等辺三角形の内角 Youtube

3

二等辺三角形の定義と性質 問題の解き方 数学fun

数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ

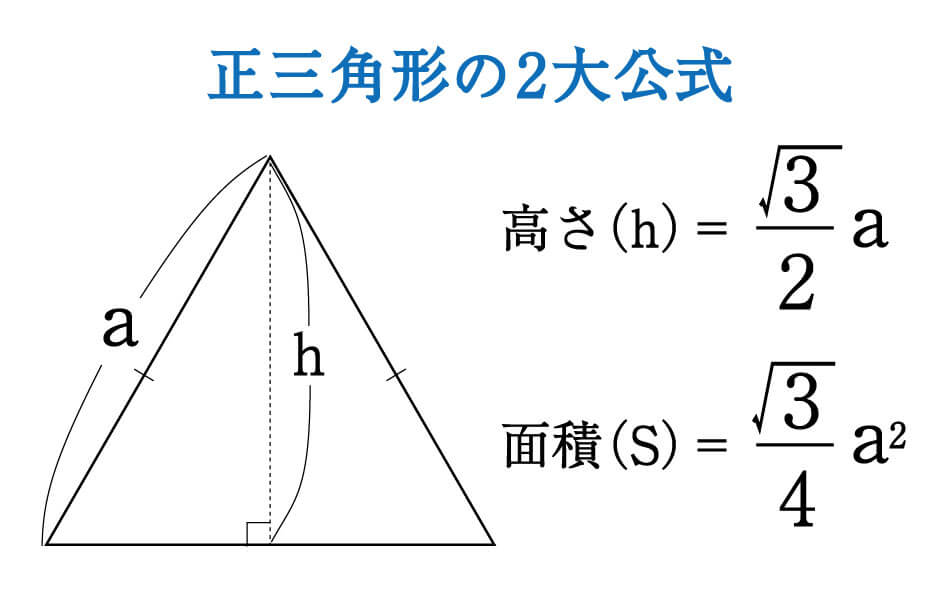
数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

高校数学a 三角形の重心 外心 垂心の位置関係 オイラー線 の幾何的証明 受験の月

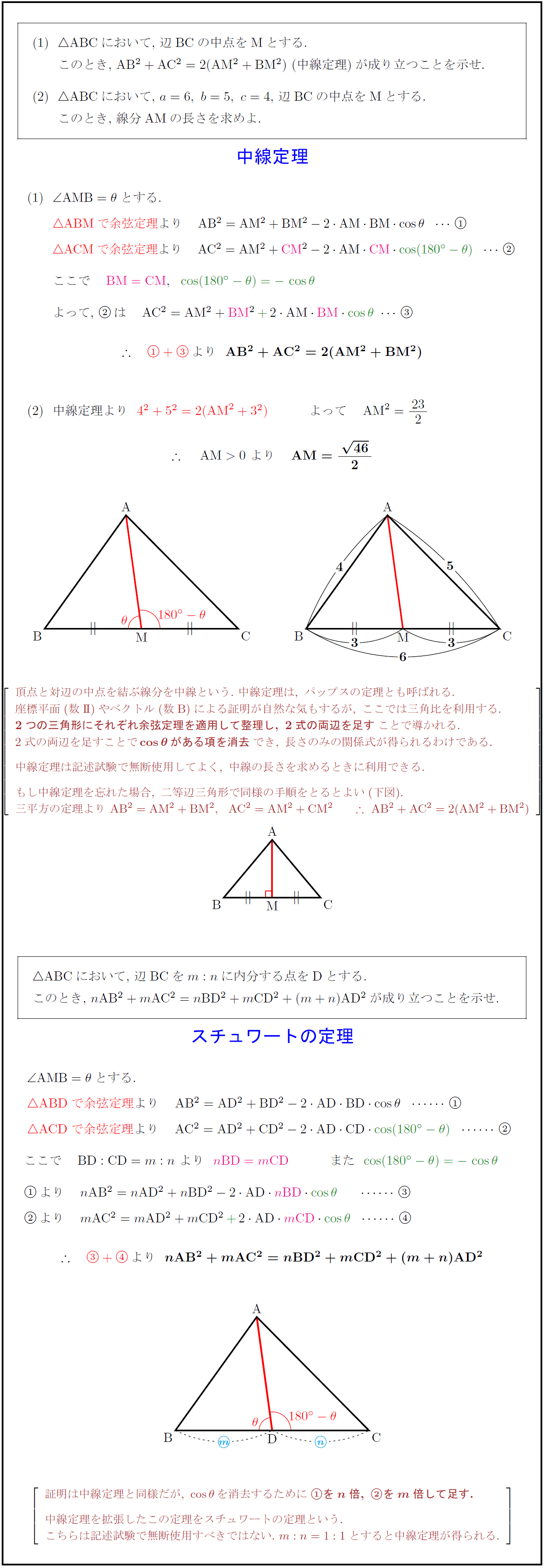
高校数学 中線定理 パップスの定理 とスチュワートの定理の三角比による証明 受験の月

二等辺三角形の公式 面積 高さ 角度 斜辺と周囲の長さ 数学 エクセルマニア

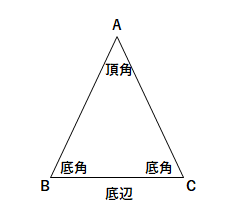
中2数学 二等辺三角形の定義と性質 Examee

二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

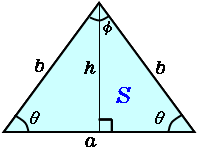
二等辺三角形 高精度計算サイト

3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく

Mathematics 三平方の定理 ３ いろいろな三角形 働きアリ

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

1

My Math Note

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典

この問題を証明する時に二等辺三角形の定理や定義は使って良いんですか Clearnote

ピタゴラスの第２定理発見 三平方根の定理 直角三角形の菅数論の定理 発想力教育研究所 素数誕生のメカニズム

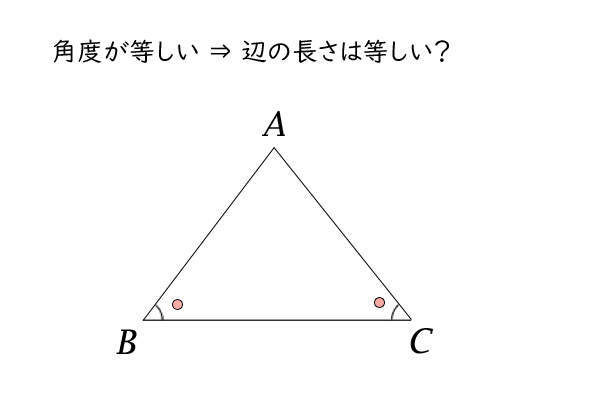
三角形の辺の長さと角の大きさの関係 高校数学マスター

Studydoctor二等辺三角形や台形の面積と三平方の定理 中学３年数学 Studydoctor

世界一わかりやすい数学問題集中２ ５章 図形の性質と証明

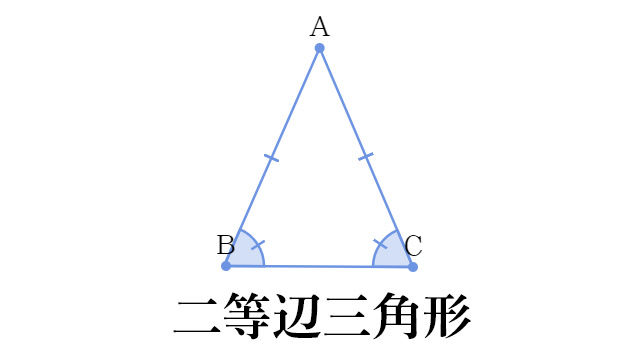
今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

二等辺三角形の頂角の角度を求めよ 解答編その2 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

Clearnote 勉強ノートまとめ Twitterren こんばんは 今日は友達とuberしようと思ったらドライバーさんみんな出払ってました 雪だからかな 今日紹介するのは 確認 三平方の定理 直角 二等辺三角形 スクールieさんのノート 大事なところだから

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

スタディピア 図形

二等辺三角形の内接円 外接円に関する問題 ２０１９年度前期日程の岡山大学文系の入試問題 身勝手な主張

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

二等辺三角形の性質 Youtube

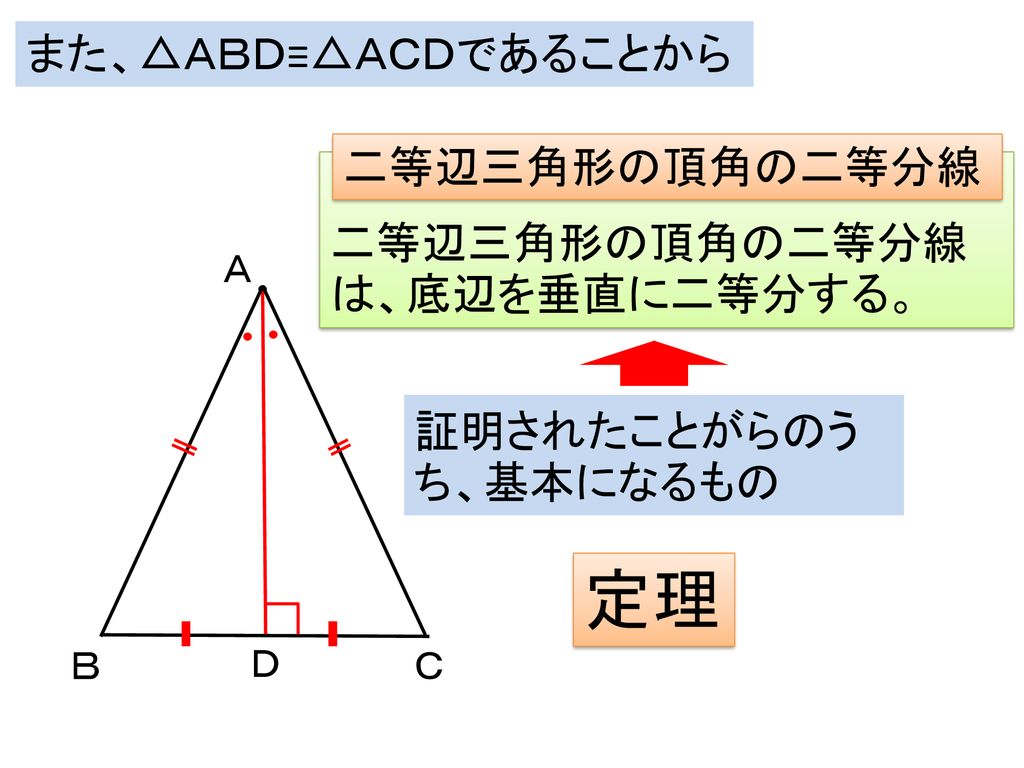
本時のねらい 二等辺三角形の作図から証明を使って性質を導くことができる 定義や定理の用語の意味を理解する Ppt Download

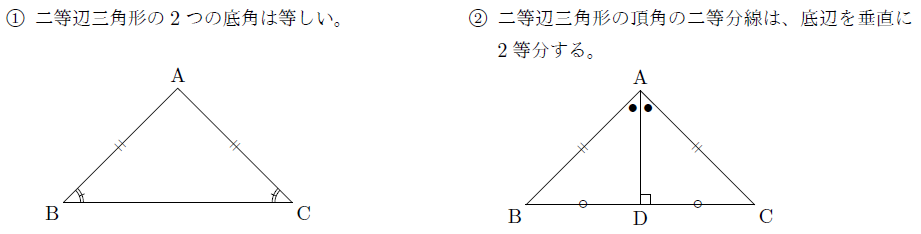
二等辺三角形の性質 まなびの学園

Cos36 解法２種類 倍角の公式利用 と 二等辺三角形で余弦定理 マスマス学ぶ

二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典

私立中学入試対策 角度の問題 二等辺三角形 外角の定理 個人契約 福岡 家庭教師 ふなきち

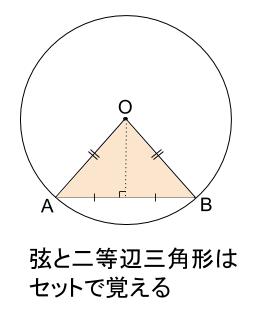
中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su

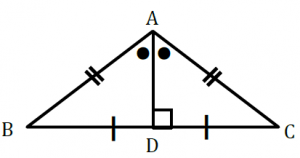
中２数学 図形の中でも重要なものの１つ 二等辺三角形について徹底解説 まなビタミン

1

二等辺三角形と正三角形 算数用語集

三角形のペア 大田 桐光本部校 ブログ

中2 二等辺三角形になるための条件 中学生 数学のノート Clearnote

二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者

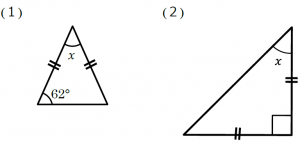
中２数学 図形の中でも重要なものの１つ 二等辺三角形について徹底解説 まなビタミン

第１巻命題５ 二等辺三角形の底角は等しい Stoixeia ストイケイア

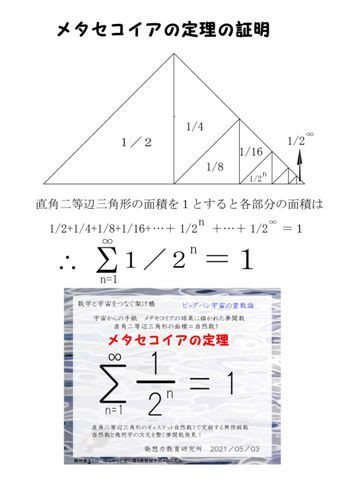
メタセコイアの定理 自然数と直角二等辺三角形の面積を繋ぐ無限級数発見 発想力教育研究所 素数誕生のメカニズム

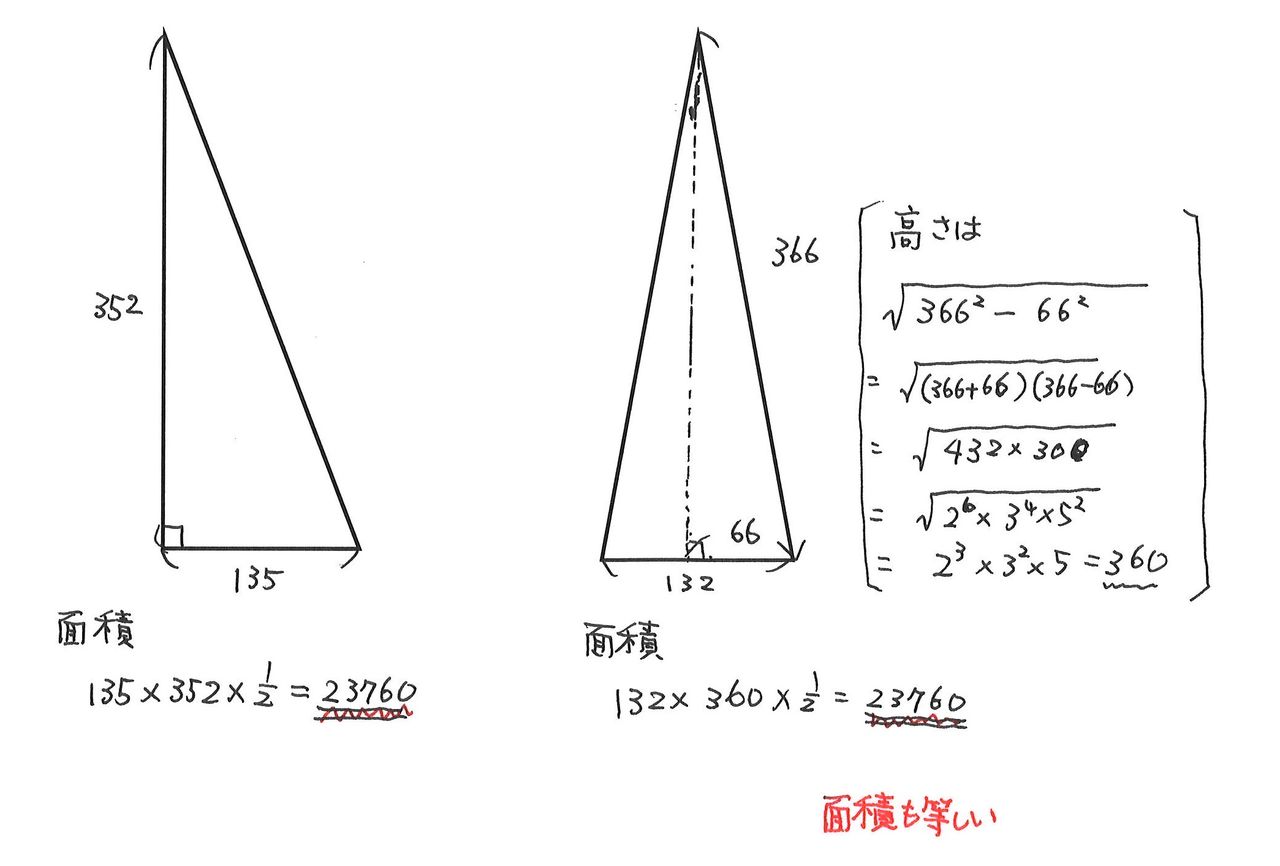
世界に１ペアだけ 周りの長さも面積も同じ直角三角形 二等辺三角形 慶大院生ペア証明 朝日新聞デジタル

中2 中2 数学 二等辺三角形など 中学生 数学のノート Clearnote

二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4

二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学

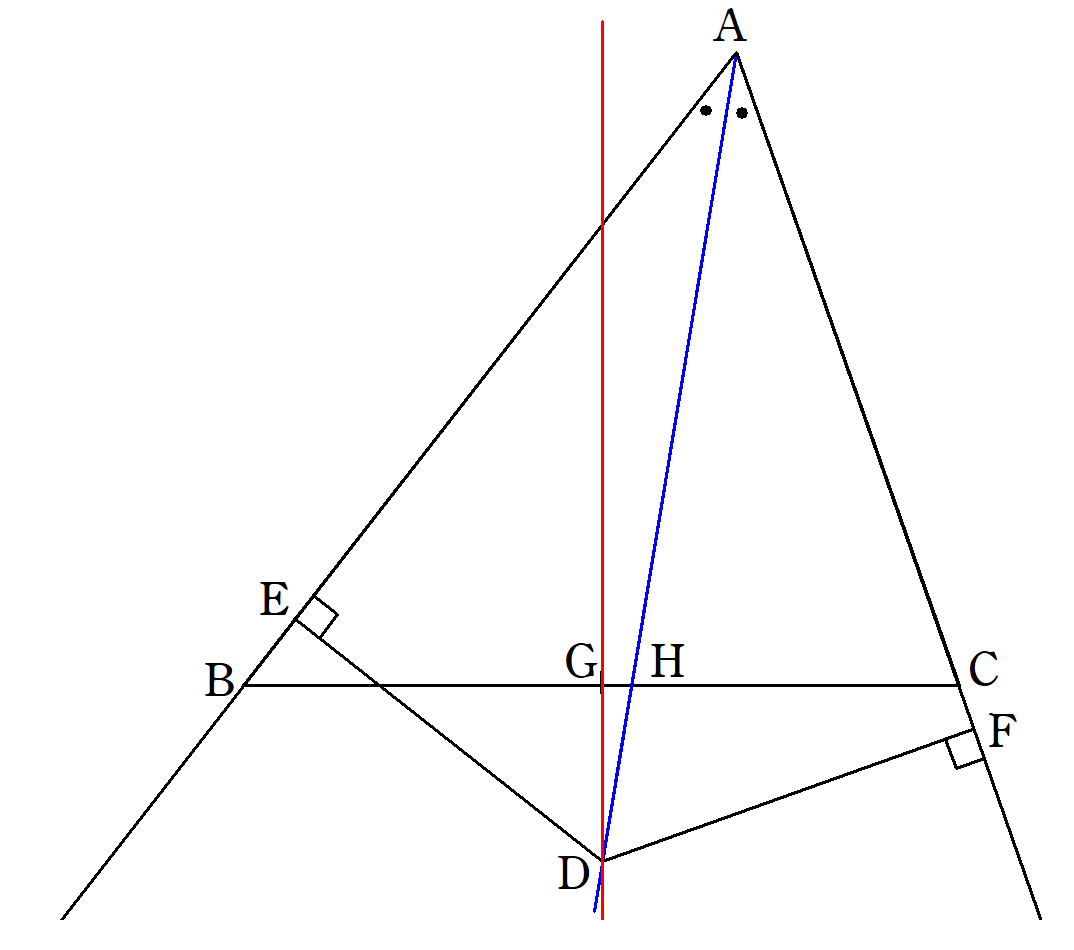
二等分線と垂線の定理 Fukusukeの数学めも

Kelas 8 Catatan Tentang 数学 中2 定義と定理 Clearnote

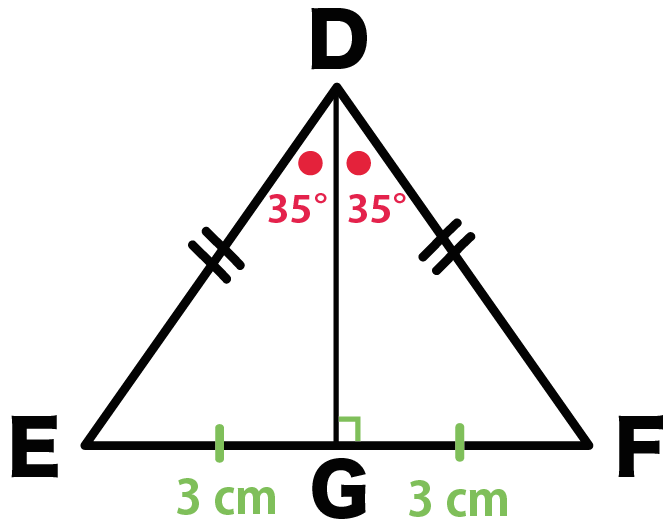
3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく

最近発見された三角形に関する定理 Meauky Blog

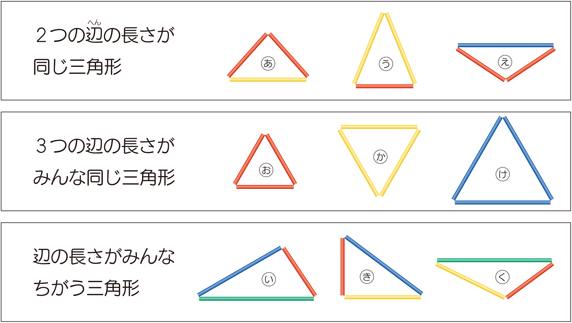
二等辺三角形と正三角形 算数用語集

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ

中学生の数学 Xyz

中2数学 二等辺三角形の性質２ 頂角の二等分線 練習編 映像授業のtry It トライイット

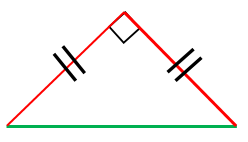
直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

二等辺三角形 Wikipedia

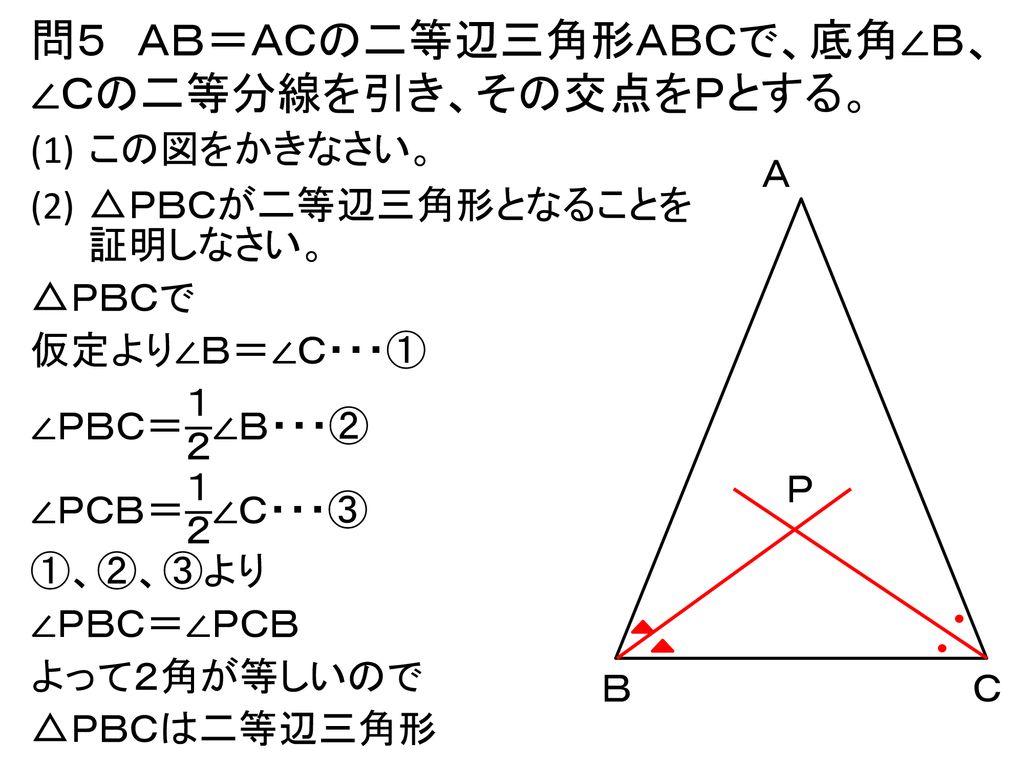
本時のねらい 二等辺三角形の作図から証明を使って性質を導くことができる 定義や定理の用語の意味を理解する Ppt Download

二等辺三角形の性質と証明 無料で使える中学学習プリント

Happylilac Net

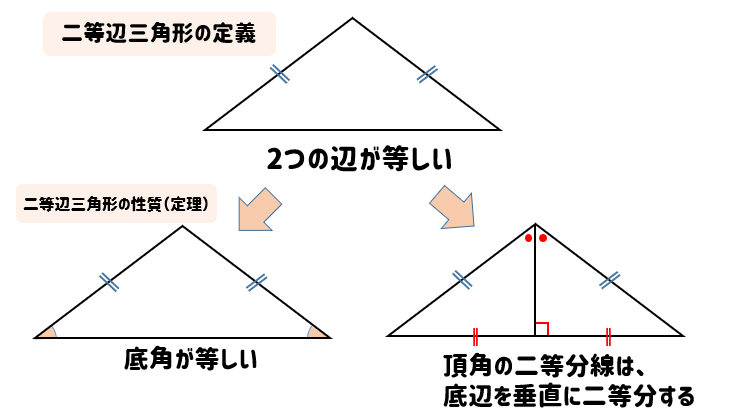
二等辺三角形の定義と性質をサクッと確認しておこう 数スタ

定義と定理の違い 中学数学 定期テスト対策 ベネッセ教育情報サイト

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

はしご直角三角形

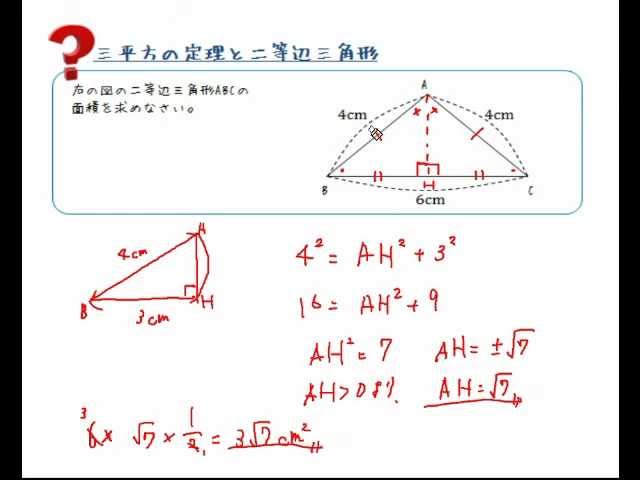
三平方の定理と二等辺三角形 Youtube

二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学

中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット

تويتر 中学高校数学laf先生 質問回答中 على تويتر 中2数学 二等辺三角形の性質 ここでは 定義 と 定理 という小難しい言葉が出てきますね O O 定義 言葉の意味を丁寧に説明したものだよ 二等辺三角形の定義 二つの辺が等しい

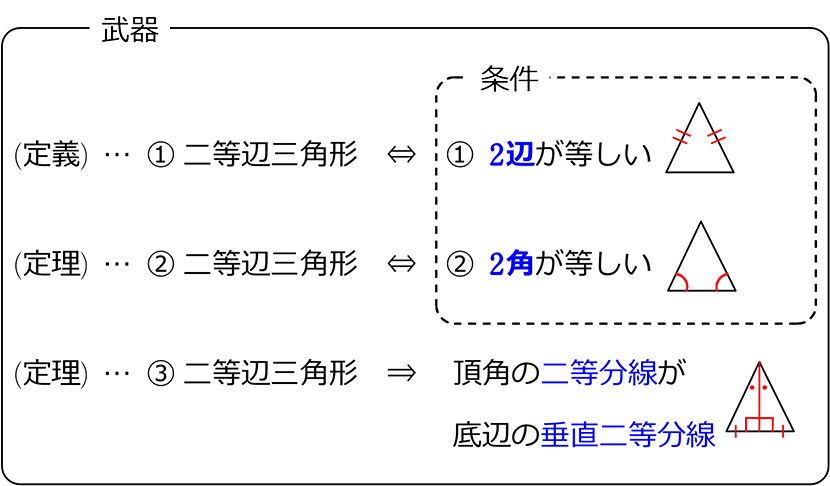
中学数学 図形の合同 図形の性質

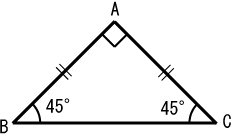
直角二等辺三角形 Wikipedia

2 54第４章 二等辺三角形 二等辺三角形の性質 ニュージーランド短期留学ダイアリー

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ